Conservation

Let us review the main reason why conservation and high efficiency— which are meritorious goals—cannot solve any hypothetical energy crisis. If there is a finite supply of energy, it will eventually run out no matter how frugal we are. If the supply would last 25 years at current rates of consumption, it would last 50 years if consumption were cut in half and 100 years if consumption were cut to one quarter. Or, if we suddenly cut all consumption of coal, oil, and natural gas by 83% (remember the House of Representatives plan to cut CO2 emissions by 83% by 2050), the 25-year fuel supply would last 150 years. Those times are very small compared to the time that has elapsed since the Roman Empire, and utterly minuscule measured against the time since Neanderthals went extinct.

In other words, given a finite and small energy supply, conservation is only a time-buying operation. Indeed, if we committed national suicide by using no energy whatsoever, the rest of the world would gobble up that small amount of energy we left for them in no time.

If, on the other hand, we rely on solar energy—a very dilute source— then we have a continuing feeble supply of energy. We can gather it slowly, but the source lasts forever. Under those conditions, very limited usage and very high efficiency are necessary for survival.

We need not adopt such extreme measures, because there is no shortage of energy (and never will be, because nuclear energy can supply all the energy for all of civilization as long as humans inhabit the earth); that conservation and high efficiency would not solve the problem if it existed; and that renewable energy (as commonly understood) would not solve the problem anyway.

On the other hand, nuclear energy is not readily adaptable for transportation. We don’t presently have any easy way to manufacture transportation fuels from heat and electricity, so therein lies a problem that will eventually have to be solved.

Lasers, Mössbauer, and Pablo Casals

Pablo Casals (December 29, 1876 – October 22, 1973) was a great cello player, but he did not play staccato. The reason lies in physics, not in the nimbleness of Casals’ fingers.

The speed of sound is about 330 meters per second. If a note is played for one second, the front of the wave travels 330 meters before the note is finished. If it is played for one hundredth of a second, the front of the wave travels 3.3 meters before the note is finished.

Suppose that the frequency of the note is 128 cycles per second (low C); then the wavelength is 330/128 = 2.6 meters. One octave down, the wavelength is 5.2 meters. So if Mr. Casals were to play that note for one hundredth of a second, the wavelength would be longer than the entire wave train, and would have a pitch unrecognizable to the ear.

The general relationship is that there is an inverse relationship between the accuracy of the frequency and the length of time the note is played.

For atoms and nuclei emitting radiation, the same rule applies, but it is usually expressed as an inverse relationship between the precision of the energy and the lifetime of the excited state that gives rise to the radiation. Lasers owe their precise wavelength to the fact that certain “forbidden transitions” cause some excited states to be long-lived. The Mössbauer effect in certain nuclei has such a sharp resonance that the Doppler effect caused by a velocity of a few millimeters per second can determine whether a sample can absorb the gamma emitted by another nucleus.

We will use that principle to expand on TEA February 2010, which talked about the probability that CO2 radiates its internal energy away, vs. losing it via collisions. Figure 1 shows the absorption spectrum of CO2, and here we pay attention to the width of the spectral lines, which turns out to be about 0.024 micro-meters (μm). That number is sufficient to tell us that the lifetime of the CO2 excited state is about 2.1 picoseconds (ps).

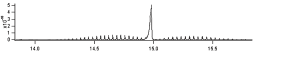Figure 1: The absorption spectrum of CO2 relevant to the “greenhouse” effect. The horizontal axis is wavelength in micro-meters. Of interest here is the width of each of the spectral lines, which is about 0.024 micro- meters.

By comparison, we can use the kinetic theory of gases and reasonable estimates of molecular sizes to estimate that the mean distance a molecule travels before hitting another is about 80 nanometers at sea-level pressure, and a mean time between collisions is roughly 20 to 25 ps, about 100 times the lifetime of the excited state.

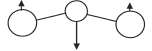Figure 2: The bending mode of the CO2 molecule. The carbon atom is the central atom, and the outer ones are oxygen. This vibration is set in motion by the absorption of IR in the 15-μ band.

In other words, a CO2 molecule that has absorbed IR has about 100 times as much likelihood of re-emitting that IR in some random direction as it has of dissipating that energy as heat via collisional de-activation. IR absorbed by CO2 does not cause appreciable heating of the atmosphere.

Incidentally, the “vibrational” mechanism that is excited by the 15-μm IR is a bending mode, as shown in Fig. 2.